面试题经典跳台阶问题



面试题经典跳台阶问题。

题目：

给定一个有N个台阶的楼梯，一个人从下到上开始跳台阶，这个人有两种跳的方式：一次跳一个台阶，一次跳两个台阶；

问：从台阶底端跳到台阶顶端，有多少种跳台阶的方式？

分析：

首先我们考虑最简单的情况。如果只有1个台阶，那么显然只有一种跳法；如果是2级台阶，那么有2种跳法。对于一个有n级台阶的楼梯来说，我们设跳法为 f(n) ，假如我们先跳1个台阶，则剩下有 n-1 个台阶，跳法为 f(n-1) 次，假如我们先跳2个台阶，则剩下 n-2 阶，跳法为 f(n-2)；由此可以推出，对于一个n阶的楼梯，有以下这个跳台阶的公式：


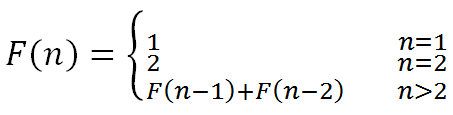
代码如下：

 

  1. #include <iostream>
  2. using namespace std;
  4. int JumpStep(int n)
  5. {
  6.     if(n <= 0)
  7.         return -1;
  8.     if(n == 1)
  9.         return 1;
  10.     if(n == 2)
  11.         return 2;
  12.     return JumpStep(n-1)+JumpStep(n-2);
  13. }
  14. int main()
  15. {
  16.     cout<<”5 step jumps : ”<<JumpStep(5)<<endl;
  17.     return 0;
  18. }

扩展： 

当跳台阶的选择多了呢？比如说 每次可以跳3个台阶；按照同样的方法分析，如下公式：

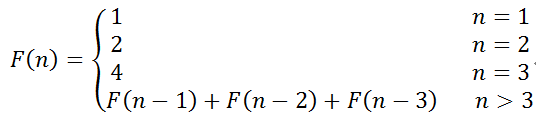
解题代码如下：

 

  1. /**
  2. 题目描述：
  3. 有N个台阶，一个人从台阶下向上跳台阶，有两种跳的选择
  4. 1次跳一个台阶，1次跳两个台阶 这两种选择；
  5. */
  6. #include <iostream>
  7. using namespace std;
  9. int JumpStep(int n)
  10. {
  11.     if(n <= 0)
  12.         return -1;
  13.     if(n == 1)
  14.         return 1;
  15.     if(n == 2)
  16.         return 2;
  17.     return JumpStep(n-1)+JumpStep(n-2);
  18. }
  19. int JumpStep3(int n)
  20. {
  21.     if(n <= 0)
  22.         return -1;
  23.     if(n == 1)
  24.         return 1;
  25.     if(n == 2)
  26.         return 2;
  27.     if(n == 3)
  28.         return 4;
  29.     return JumpStep3(n-1)+JumpStep3(n-2)+JumpStep3(n-3);
  30. }
  31. int main()
  32. {
  33.     cout<<”5 step jumps : ”<<JumpStep(5)<<endl;
  34.     cout<<”5 step jumps : ”<<JumpStep3(5)<<endl;
  35.     return 0;
  36. }