Google面试题:统计1~N中所包含的1的个数



Google面试题:统计1~N中所包含的1的个数，

题目：

输入：一个正整数N，

输出：要求输出从 1 ~ N 中所出现的 1 的个数，如12中所包含的 1 的数为： 1  、10、11、12 总共包含 5个 1

解法1：

可以对从1~N的每个数字进行遍历，分别求出每个数字中所包含的1的个数，然后相加求和即可得出最后结果；

如下代码：

 

  1. #include <iostream>
  2. using namespace std;
  4. int coutOne(unsigned int n)
  5. {
  6.     int num=0;
  7.     while(n)
  8.     {
  9.         if(n%10==1)
  10.             num++;
  11.         n=n/10;
  12.     }
  13.     return num;
  14. }
  15. int coutNNum(unsigned int n)
  16. {
  17.     int numb = 0;
  18.     int i = 1;
  19.     for(i=1;i<=n;i++)
  20.         numb += coutOne(i);
  21.     return numb;
  22. }
  24. int main()
  25. {
  26.     int n;
  27.     while(cin>>n)
  28.         cout<<”\nnumber of 1 is : ”<<coutNNum(n)<<endl;
  29.     return 0;
  30. }

说明：这种解法有个明显的缺陷，就是时间复杂度为O(n)，假如说N的值足够大，计算过程中消耗的时间很多，以下是一种缩减时间复杂度的算法。

 

解法2：

在解题之前，我们先对题目进行分析，找一下规律：

对于一个数  2134 ；我们将其分解为两段： 1 ~ 134 和135 ~ 2134 ；分别求出这两段中1的个数，即可求出总的1的个数。首先对于 两段进行分析，先拿第二段来说：135 ~ 2134 中 1 的出现的规律如下： 当千位为1 时 ，这个 1 出现的个数为1000次，即从1000 ~ 1999 千位的1 总共出现了 1000 次，即 出现了 10^3 次；标记为：numFirstDigit

最高位考虑过之后，然后对其他位进行考虑，其他位中 1 出现的个数的计算方法为：

最高位数值为：2      剩余的位数为：3       135~2134中总共个数为：2000个

则这2000个数中，出最高位 1 有1000个之外，其余位的 1 的个数为：　2 * 3 * 10^2


对于这个数的理解为：最高位数值为2 表示最高位有两种选择 1或2；统计 后 3 位中 1 的个数为：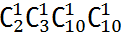 

    用排列组合的思想来理解。

此处计算出了 135 ~ 2134 中 1的个数了 标记为 ： numOtherDigits =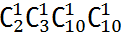 

 

接下来计算第一段 1 ~ 134 中1的个数，对于这段，我们再将其分解 ，分解为 1~34 和 35 ~134 ，利用递归的思想解题。

对于1 ~ 134 中包含的1的个数标记为： numRecursive

至此 对这道题的思想已经解释清楚 ，对于 numFirstDigit  的值的判断如下

如果 最高位 大于 1，则最高位 1 包含1的个数为：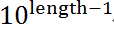

如果最高位 等于  1，则最高位 1 包含1的个数为：如 1134 ，则 千位包含1的个数为 1134 – 1000 + 1 = 135

代码如下：

 

  1. #include <iostream>
  2. #include <math.h>
  3. using namespace std;
  5. int pow10(int n);
  6. //计算N的位数
  7. int coutLength(int num)
  8. {
  9.     int length = 0;
  10.     while(num!=0)
  11.         length++,num = num/10;
  12.     return length;
  13. }
  14. int recuriveCoutNumOfOne(int n)
  15. {
  16.     int length = coutLength(n); //存储 n 的位数
  17.     if( n <= 0)
  18.         return 0;
  19.     if(n>0 && n<10)
  20.         return 1;
  22.     //拿 2134来分析
  23.     //存储高位的数值 2
  24.     int numFirstValue = n/pow10(length-1);
  25.     //存储高位中有1的个数
  26.     int numFirstDigit = 0;
  27.     //存储其他位中有1的个数
  28.     int numOtherDigit;
  29.     numOtherDigit = numFirstValue * (length-1) * pow10(length-2);
  30.     //存储 第一段 1 ~ 134 中的1的个数
  31.     //cout<<”\n后几位为:”<<n%((int)pow(10,length))<<endl;
  32.     int numRecuive = recuriveCoutNumOfOne(n%pow10(length-1));
  33.     //接下来对最高位为 来分析
  34.     if(numFirstValue > 1)
  35.         numFirstDigit = pow10(length);
  36.     if( numFirstValue == 1)
  37.         numFirstDigit = n - pow10(length-1)+1;
  38.     return numFirstDigit + numOtherDigit + numRecuive;
  39. }
  40. int pow10(int n)
  41. {
  42.     int num=1;
  43.     while(n)
  44.         num *=10,n–;
  45.     return num;
  46. }
  49. int main()
  50. {
  51.     cout << ”Hello world!” << endl;
  52.     int n;
  53.     while(cin>>n)
  54.         cout<<”\nnum of one is : ”<<recuriveCoutNumOfOne(n)<<endl;
  55.     return 0;
  56. }

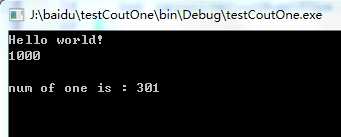
运行结果：