c++位图排序图文介绍



c++位图排序图文介绍。

一.位图排序的应用：

1.给40亿个不重复的unsigned int的整数，没有排过序，然后再给一个数，如果快速判断这个数是否在那40亿个数当中。

因为unsigned int数据的最大范围在在40亿左右，40*10^8/1024*1024*8=476，因此只需申请512M的内存空间，每个bit位表示一个unsigned int。读入40亿个数，并设置相应的bit位为1.然后读取要查询的数，查看该bit是否为1，是1则存在，否则不存在。

2.给40亿个unsigned int的整数，如何判断这40亿个数中哪些数重复？

同理，可以申请512M的内存空间，然后读取40亿个整数，并且将相应的bit位置1。如果是第一次读取某个数据，则在将该bit位置1之前，此bit位必定是0；如果是第二次读取该数据，则可根据相应的bit位是否为1判断该数据是否重复。

 

 

二.位图排序的实现

由于在C语言中没有bit这种数据类型，因此必须通过位操作来实现。

假如有若干个不重复的正整数，范围在[1-100]之间，因此可以申请一个int数组，int数组大小为100/32+1。

 

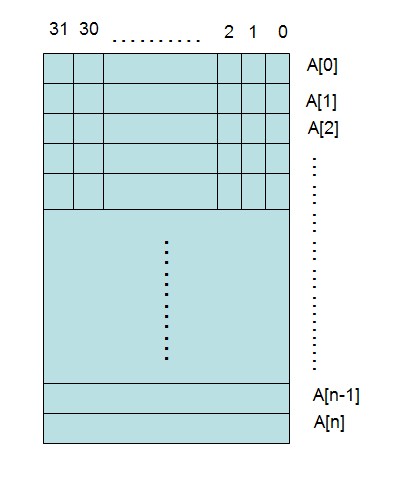
假如有数据32，则应该将逻辑下标为32的二进制位置1，这个逻辑位置在A[1]的最低位(第0位)。

因此要进行置1位操作，必须先确定逻辑位置：字节位置(数组下标)和位位置。

字节位置=数据/32;(采用位运算即右移5位)

位位置=数据%32;(采用位运算即跟0X1F进行与操作)。

其他操作如清0和判断两个操作类似。

C语言实现程序:

 

[cpp] view plaincopy


  1. /*位图排序 2011.10.18*/
  2. #include <stdio.h>
  3. #define MAX 1000000
  4. #define SHIFT 5
  5. #define MASK 0x1F
  6. #define DIGITS 32
  7. int a[1+MAX/DIGITS];
  9. void set(int n)     //将逻辑位置为n的二进制位置为1
  10. {
  11.     a[n>>SHIFT]=a[n>>SHIFT]|(1<<(n&MASK));     //n>>SHIFT右移5位相当于除以32求算字节位置，n&MASK相当于对32取余即求位位置，
  12. }                                              //然后将1左移的结果与当前数组元素进行或操作，相当于将逻辑位置为n的二进制位置1.
  14. void clear(int n)
  15. {
  16.     a[n>>SHIFT]=a[n>>SHIFT]&(~(1<<(n&MASK)));   //将逻辑位置为n的二进制位置0，原理同set操作
  17. }
  19. int test(int n)
  20. {
  21.     return a[n>>SHIFT] & (1<<(n&MASK));        //测试逻辑位置为n的二进制位是否为1
  22. }
  24. int main(int argc, char *argv[])
  25. {
  26.     int i,n;
  27.     for(i=1;i<=MAX;i++)
  28.     {
  29.         clear(i);
  30.     }
  31.     while(scanf(“%d”,&n)!=EOF)
  32.     {
  33.         set(n);
  34.     }
  35.     for(i=1;i<=MAX;i++)
  36.     {
  37.         if(test(i))
  38.             printf(“%d ”,i);
  39.     }
  40.     return 0;
  41. }

 

 

在C++中提供了bitset这种集合，专门用来进行位操作，因此实现起来比较容易

C++版本：

 

  1. /*位图排序C++STL实现 2011.10.19*/
  2. #include <iostream>
  3. #include<bitset>
  4. #define MAX 1000000
  5. using namespace std;
  7. bitset<MAX+1> bit;        //声明一个有(MAX+1)个二进制位的bitset集合，初始默认所有二进制位为0
  9. int main(int argc, char *argv[])
  10. {
  11.     int n,i;
  12.     while(scanf(“%d”,&n)!=EOF)
  13.     {
  14.         bit.set(n,1);          //将第n位置1
  15.     }
  16.     for(i=0;i<=MAX+1;i++)
  17.     {
  18.         if(bit[i]==1)
  19.             printf(“%d ”,i);
  20.     }
  21.     return 0;
  22. }