c++有向图中顶点的路径问题

c++有向图中顶点的路径问题。

主要解决三个问题：

前提：有向图+邻接矩阵存储

问题1、判断有向图中是否存在顶点u到v的路径

问题2、求u到v的所有简单路径

问题3、求u到v长度为k的简单路径

具体如下：

问题1：判断有向图中是否存在顶点u到v的路径

方法：可以使用深度遍历或广度遍历

源代码：

[cpp] view plain copy

#include <iostream>
using namespace std;
const int MAX_Vertex_Num = 20;
template<class VexType,class ArcType>
class MGraph
{
public:
void CreateGraph();//创建图
int LocateVex(VexType v);//返回顶点v所在顶点向量中的位置（下标）
bool getPathiToj(VexType u1,VexType u2);
private:
VexType vexs[MAX_Vertex_Num];//顶点向量
ArcType arcs[MAX_Vertex_Num][MAX_Vertex_Num];
int vexnum;//顶点数
int arcnum;//边数
private:
void getPathiToj_DFS(int x,int y,int num,bool& isFind,bool visited[MAX_Vertex_Num],int path[MAX_Vertex_Num]);//借助DFS的思想实现
};
template<class VexType,class ArcType>
void MGraph<VexType,ArcType>::CreateGraph()
{
VexType first;
VexType Secend;
cout<<”请输入顶点数:”;
cin>>vexnum;
cout<<”请输入边数:”;
cin>>arcnum;
cout<<”请输入各个顶点值：”;
for (int i=0;i<vexnum;i++)
{
cin>>vexs[i];
}
//初始化邻接矩阵
for (int i=0;i<arcnum;i++)
{
for (int j=0;j<arcnum;j++)
{
arcs[i][j]=0;
}
}
cout<<”请输入边的信息:”<<endl;
for (int i=0;i<arcnum;i++)
{
cin>>first>>Secend;
//如果边有权值的话，则还应该输入权值
int x = LocateVex(first);
int y = LocateVex(Secend);
arcs[x][y]=1;//如果是有权的话，这里应该是arc[x][y]=权值
//arcs[y][x]=1;//无向图是对称的
}
}
/*
参数：v：表示顶点向量中一个值
函数返回值：函数返回v在顶点向量中的下标
*/
template<class VexType,class ArcType>
int MGraph<VexType,ArcType>::LocateVex(VexType v)
{
for (int i=0;i<vexnum;i++)
{
if (vexs[i]==v)
{
return i;
}
}
return -1;
}
/*
返回顶点u1到u2之间的路径
参数：
u1:表示起始顶点
u2:表示终点顶点
*/
template<class VexType,class ArcType>
bool MGraph<VexType,ArcType>::getPathiToj(VexType u1,VexType u2)
{
bool isFind=false;
int num=0;//两个顶点存在路径时，之间的顶点数
int x = LocateVex(u1);
int y = LocateVex(u2);
bool visited[MAX_Vertex_Num]={false};
int path[MAX_Vertex_Num];
visited[x]=true;
path[0]=x;
getPathiToj_DFS(x,y,num+1,isFind,visited,path);
return isFind;
}
/*
返回 x指向的起始顶点到 y指向的终点顶点的所有路径
参数：
x表示起始顶点的坐标，一直在变化
y表示终点顶点的坐标，一直保持不变
num：现在路径中的顶点个数
visited数组:表示每个顶点是不是已经访问过
path数组：用来存放每条路径
*/
template<class VexType,class ArcType>
void MGraph<VexType,ArcType>::getPathiToj_DFS(int x,int y,int num,bool& isFind,bool visited[MAX_Vertex_Num],int path[MAX_Vertex_Num])
{
for (int j=0;j<vexnum;j++)
{
if (arcs[x][j]==1 && visited[j]==false)
{
path[num]=j;//每遇到一个顶点都要该顶点都放到数组中
visited[j]=true;
if (j==y)//到达目的节点，输出路径
{
isFind = true;
cout<<”顶点”<<vexs[0]<<”到”<<vexs[j]<<”的路径为:”;
for (int i=0;i<num+1;i++)
{
cout<<vexs[path[i]];
}
cout<<endl;
//找到终点，此时本次查找结束
}
else//当没有找到时，要继续往下一层寻找
{
getPathiToj_DFS(j,y,num+1,isFind,visited,path);//无论此时找没找到终点，总是要往下走的
}
visited[j]=false;//回溯，恢复现场。当走下一次循环时，要把上一次递归过程中访问到的结点都恢复到起始状态，重新处理
}
}
}
int main()
{
MGraph<char,int> G;
G.CreateGraph();
if (!G.getPathiToj(‘A’,'J’))
{
cout<<”A到J之间不存在路径！”<<endl;
}
if (!G.getPathiToj(‘A’,'G’))
{
cout<<”A到G之间不存在路径！”<<endl;
}
system(“pause”);
return 1;
}

结果测试：

有向图：

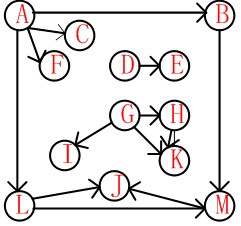
输出结果：

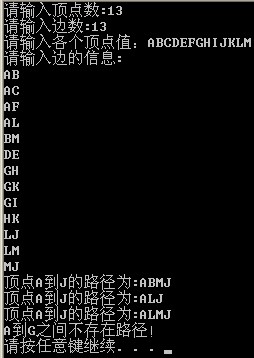
问题3、

方法：使用回溯法

源代码：

[cpp] view plain copy

#include <iostream>
using namespace std;
const int MAX_Vertex_Num = 20;
template<class VexType,class ArcType>
class MGraph
{
public:
void CreateGraph();//创建图
int LocateVex(VexType v);//返回顶点v所在顶点向量中的位置（下标）
bool getPathiToj(VexType u1,VexType u2,int k);
private:
VexType vexs[MAX_Vertex_Num];//顶点向量
ArcType arcs[MAX_Vertex_Num][MAX_Vertex_Num];
int vexnum;//顶点数
int arcnum;//边数
private:
void getPathiToj_DFS(int x,int y,int num,int k,bool& isFind,bool visited[MAX_Vertex_Num],int path[MAX_Vertex_Num]);//借助DFS的思想实现
};
template<class VexType,class ArcType>
void MGraph<VexType,ArcType>::CreateGraph()
{
VexType first;
VexType Secend;
cout<<”请输入顶点数:”;
cin>>vexnum;
cout<<”请输入边数:”;
cin>>arcnum;
cout<<”请输入各个顶点值：”;
for (int i=0;i<vexnum;i++)
{
cin>>vexs[i];
}
//初始化邻接矩阵
for (int i=0;i<arcnum;i++)
{
for (int j=0;j<arcnum;j++)
{
arcs[i][j]=0;
}
}
cout<<”请输入边的信息:”<<endl;
for (int i=0;i<arcnum;i++)
{
cin>>first>>Secend;
//如果边有权值的话，则还应该输入权值
int x = LocateVex(first);
int y = LocateVex(Secend);
arcs[x][y]=1;//如果是有权的话，这里应该是arc[x][y]=权值
//arcs[y][x]=1;//无向图是对称的
}
}
/*
参数：v：表示顶点向量中一个值
函数返回值：函数返回v在顶点向量中的下标
*/
template<class VexType,class ArcType>
int MGraph<VexType,ArcType>::LocateVex(VexType v)
{
for (int i=0;i<vexnum;i++)
{
if (vexs[i]==v)
{
return i;
}
}
return -1;
}
/*
返回顶点u1到u2之间的路径
参数：
u1:表示起始顶点
u2:表示终点顶点
*/
template<class VexType,class ArcType>
bool MGraph<VexType,ArcType>::getPathiToj(VexType u1,VexType u2,int k)
{
bool isFind=false;
int num=0;//两个顶点存在路径时，之间的顶点数
int x = LocateVex(u1);
int y = LocateVex(u2);
bool visited[MAX_Vertex_Num]={false};
int path[MAX_Vertex_Num];
visited[x]=true;
path[0]=x;
getPathiToj_DFS(x,y,num+1,k,isFind,visited,path);
return isFind;
}
/*
返回 x指向的起始顶点到 y指向的终点顶点的所有路径
参数：
x表示起始顶点的坐标，一直在变化
y表示终点顶点的坐标，一直保持不变
num：现在路径中的顶点个数
visited数组:表示每个顶点是不是已经访问过
path数组：用来存放每条路径
*/
template<class VexType,class ArcType>
void MGraph<VexType,ArcType>::getPathiToj_DFS(int x,int y,int num,int k,bool& isFind,bool visited[MAX_Vertex_Num],int path[MAX_Vertex_Num])
{
for (int j=0;j<vexnum;j++)
{
if (arcs[x][j]==1 && visited[j]==false)
{
path[num]=j;//每遇到一个顶点都要该顶点都放到数组中
visited[j]=true;
if (j==y && num==k)//到达目的节点，输出路径(num表示结点个数,k表示边的个数,但是要注意num=1时，表示有两个顶点)
{
isFind = true;
cout<<”顶点A到J之间长度为”<<k<<”的路径为： ”;
for (int i=0;i<num+1;i++)
{
cout<<vexs[path[i]];
}
cout<<endl;
//找到终点，此时本次查找结束
}
else//当没有找到时，要继续往下一层寻找
{
getPathiToj_DFS(j,y,num+1,k,isFind,visited,path);//无论此时找没找到终点，总是要往下走的
}
visited[j]=false;//回溯，恢复现场。当走下一次循环时，要把上一次递归过程中访问到的结点都恢复到起始状态，重新处理
}
}
}
int main()
{
MGraph<char,int> G;
G.CreateGraph();
for (int k=1;k<5;k++)
{
if (!G.getPathiToj(‘A’,'J’,k))
{
cout<<”顶点A到J之间不存在长度为”<<k<<”的路径！”<<endl;
}
}
system(“pause”);
return 1;
}

结果测试：

有向图：

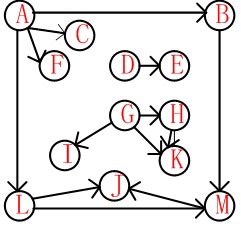
结果：

本文链接地址: c++有向图中顶点的路径问题http://www.hongyanliren.com/2014m07/11395.html

红颜丽人

追求技术就像追求#$！不抛弃，不放弃！

c++有向图中顶点的路径问题

相关文章