c 面试题之二叉搜索树与双向链表实例代码介绍。面试题目:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
二叉树结点的定义:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
下图是一个二叉树转换示例:
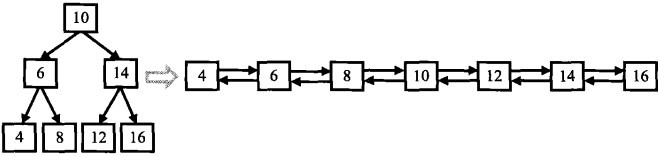
二叉树的每个结点都有两个指向子结点的指针。双向链表的每个结点也有两个指针,分别指向前一个结点和后一个结点。所以这两种结点的结构相似。
二叉搜索树是一种排序的数据结构。它的左子结点的值总是小于父结点的值,右子结点的值总是大于父结点的值。因此在转换成排序的双向链表时,原先指向左子结点的指针调整为链表中指向前一个结点的指针,原先指向右子结点的指针调整为链表中指向后一个结点的指针。
可以中序遍历树中的每一个结点,由于对于二叉搜索树来讲,中序遍历算法刚好是按照从小到大的顺序遍历树的每一个结点。当遍历转换到根结点(值为10的结点)时,它的左子树已经转换成一个排序的双向链表了,并且链表中的最后一个结点是当前值最大的结点。我们把值为8的结点和根结点链接起来,此时链表中的最后一个结点就是10了。接着遍历转换右子树,并把根结点和右子树中最小的结点链接起来。至于怎么转换它的左子树和右子树,由于遍历和转换过程是一样的,很自然的想到可以用递归。
c 面试题之二叉搜索树与双向链表代码实例如下:
BinaryTreeNode* Convert(BinaryTreeNode* pRootOfTree)
{
BinaryTreeNode *pLastNodeInList = NULL;
ConvertNode(pRootOfTree, &pLastNodeInList);
// pLastNodeInList指向双向链表的尾结点,
// 需要返回头结点
BinaryTreeNode *pHeadOfList = pLastNodeInList;
while (pHeadOfList != NULL && pHeadOfList->m_pLeft != NULL)
pHeadOfList = pHeadOfList->m_pLeft;
return pHeadOfList;
}
void ConvertNode(BinaryTreeNode* pNode, BinaryTreeNode** pLastNodeInList)
{
if (pNode == NULL)
return;
BinaryTreeNode *pCurrent = pNode;
if (pCurrent->m_pLeft != NULL)
ConvertNode(pCurrent->m_pLeft, pLastNodeInList);
pCurrent->m_pLeft = *pLastNodeInList;
if (*pLastNodeInList != NULL)
(*pLastNodeInList)->m_pRight = pCurrent;
*pLastNodeInList = pCurrent;
if (pCurrent->m_pRight != NULL)
ConvertNode(pCurrent->m_pRight, pLastNodeInList);
}
上面的代码用pLastNodeInList指向已经转换好的链表的尾结点(也就是值最大的结点)。当遍历到值为10的结点时,它的左子树已经转换好了,因此pLastNodeInList指向值为8的结点。接着把根节点链接到链表中之后,值为10的结点成了链表中的尾结点,于是pLastNodeInList指向值为10的结点。接下来把pLastNodeInList作为参数传入函数递归遍历右子树。找到右子树中最左边的子结点(值为12的结点,在右子树中值最小),并把该结点和值为10的结点链接起来。
(对ConvertNode()函数不太理解的话,最好是单步调试一下。我最初主要是觉得这段代码,只链接了根节点和左子树的转换结果。对于根节点是如何与右子树链接的不太明白。其实是这样:当转换到结点10时,我把最下面的ConvertNode()递归调用简写成:ConvertNode(14, 10);,然后代码从ConvertNode()的开始处执行,由于14->m_pLeft是结点12,所以递归执行ConvertNode(12, 10);,然后代码又从ConvertNode()的开始处执行,而此时12->m_pLeft等于NULL,所以接着执行pCurrent->m_pLeft = *pLastNodeInList;,也就是12->m_pLeft = 10;,所以此时相当于前面的根节点10,和它的右子树的最小结点12链接起来了。这个过程用文字描述起来比较困难,最好是单步执行以下,才能更好的理解。)