动态规划教程之装配线调度详细介绍（图示）。动态规划的题目练习与解答过程介绍。通过工厂最快路线的结构……

引入“动态规划”算法的例子。如下图，某公司有两条生产汽车的装配线。每一条装配线上有n个装配站，编号为j = 1,2,…,n。将装配线(i = 1,2)的第j个装配站表示为S_i,j。装配线1的第j个装配站S_1,j，与装配线2的第j个装配站S_2,j执行相同的功能，但S_1,j和S_2,j所需的装配时间可能不同。把装配站S_i,j所需的装配时间记为a_i,j。一个汽车底盘进入其中一条装配线，然后从每一站进行到下一站。底盘进入装配线的进入时间为e_i，装配完的汽车离开装配线的时间为x_i。

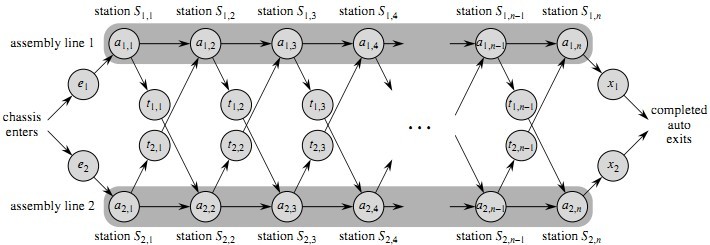
[图1]

在装配过程中，汽车可以在任何装配站上从一条装配线移到另一条装配线上。把已经通过装配线S_i,j的一个底盘从装配线i移走的时间记为t_i,j(其中i=1,2；j = 1,2,…,n-1)。现在的问题是在装配线1、2内各选择哪些装配站，使得汽车通过工程的总时间最小。例如在下图的例子中，最快的路线已经用粗体标识出来了。

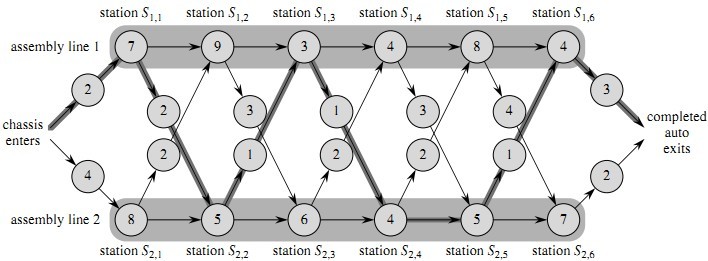
[图2]

使用强力法(brute force)来解这道题是不行的。把装配线1内使用的装配站集合看做是{1,2,…,n}的一个子集，那这样的子集将有2^n个，所以如果想穷举所有可能的方式，然后通过计算每种方式花费的时间来确定最快路线，那时间复杂度将是Ω(2^n)，这在n很大时是不可行的。

下面以动态规划的思想来解这道题。

步骤1：通过工厂最快路线的结构

动态规划的第一步是描述最优解的结构特征。考虑底盘从起点到装配站S_1,j的最快路线。如果j=1，则只有一条路线。当j=2,3,…,n时，有两种选择：(1)底盘从装配站S_1,j-1到S_1,j，因为是在相同的装配线上，所以移动的代价忽略不计。(2)底盘从装配站S_2,j-1到S_1,j，移动的代价是t_2,j-1。所以，对于装配线调度问题，一个问题的(找出通过装配站S_i,j的最快路线)最优解包含了子问题(找出通过S_1,j-1或S_2,j-1的最快路线)的一个最优解。称这个性质为最优子结构(optimal substructure)，它是是否可以应用动态规划算法的标志之一。所以，对于装配线调度问题，通过建立子问题的最优解，就可以建立原问题某个实例的一个最优解了。

步骤2：一个递归的解

动态规划的第二步是利用子问题的最优解来递归定义一个最优解的值。对于装配线的调度问题，选择在两条装配线上通过装配站j的最快路线的问题作为子问题，j=1,2,…,n。令f_i[j]表示从起点到装配站S_i,j的最快可能时间。将底盘通过工厂的所有路线的最快时间记为f*。

f₁[1]和f₂[1]的计算相对简单，因为底盘是直接到达该装配站的。

而当j=2,3,…,n时：

合并公式(15.2)~(15.5)：

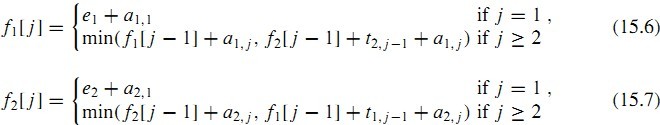
下图计算了图2中示例的f_i[j]值，以及f*的值：

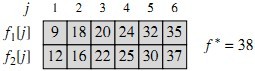
[图3]

f_i[j]的值就是子问题最优解的值。

为了助于跟踪最优解的构造过程，定义l_i[j]为装配线的编号，假设l_i[j]=1，则S₁[j-1]被装备站S_i,j的最快路线所使用。定义l*为这样的装配线：S_l*n被通过整个工厂的最快路线所使用。l_i[j]的值可以帮助找到一个最快的路线。

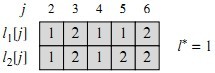
下图计算了图2中示例的l_i[j]值，以及l*的值：

[图4]

从l*=1开始，使用装配站S_1,6，而l₁[6]=2，所以使用装配站S_2,5，而l₂[5]=2，所以使用装配站S_2,4，……，以此类推。

步骤3：计算最快时间

基于公式(15.1)、(15.6)、(15.7)可以很容易的写出一个递归算法，但这样的递归算法的复杂度是指数级的。设r_i(j)为递归算法中引用f_i[j]的次数，则有：

可以证明r_i(j)=2^n-j，这样单是f₁[1]就被引用了2^n-1次，而f_i[j]总的被引用次数为theta(2^n)。

从上面的讨论、公式以及图示中，已经知道f_i[j]的每一个值依赖于f₁[j-1]和f₂[j-1]，所以可以通过递增装配站编号j的顺序来计算f_i[j]的值。即在图3中从左到右，可以在theta(n)时间内计算出最快路线，及其所花的时间。下面是参考(伪)代码：

FASTEST-WAY的工作方式如下：第1~2行利用公式(15.2)、(15.3)来计算f₁[1]和f₂[1]。第3~13行的for循环计算f_i[j]和l_i[j]，i=1,2，j=2,3,…,n。第4~8行利用公式(15.4)来计算f₁[i]和l₁[j]，第9~13行利用公式(15.5)来计算f₂[j]和l₂[j]。最后，第14~18行利用公式(15.1)来计算f*和l*。整个过程总的时间复杂度是theta(n)。

这个函数的工作过程，就像是在图3和图4中从左到有进行填表，要填入一个记录f_i[j]时，需要f₁[j-1]和f₂[j-1]的值，而它们的值已经计算并保存在表中了，只需要查询而不需要重新计算了。

步骤4：构造通过工厂的最快路线

计算出f_i[j]、f*、l_i[j]、l*之后，就可以利用l_i[j]和l*构造出最快路线所使用的装配站序列：

这段代码以站号递减的顺序输出所有的装配站。

《Introduction to Algorithms》笔记