c++算法练习题之计算连续子数组的最大和。以及动态规划的简单使用实例。

题目：输入一个整形数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组,求所有子数组的和的最大值。要求时间复杂度为O(n)。

例如输入的数组{1, -2, 3, 10, -4, 7, 2, -5}，和最大的子数组为{3, 10, -4, 7, 2}，因此输出为该子数组的和18。

如果不考虑时间复杂度，可以枚举出数组的所有子数组并求出它们的和。长度为n的数组，共有n(n+1)/2个子数组。计算所有子数组的和，最快也需要O(n^2)的时间。本题还有更快的解法。

解法一：分析规律

当加上一个正数时，和会增加；当加上一个负数时，和会减少。如果当前得到的和是个负数，那么这个和在接下来的累加中应该抛弃，不然的话这个负数将会减少接下来的和。用变量nCurSum存储当前的累加和，用nGreatestSum存储历史最大的累加和。

bool g_InvalidInput = false;

int FindGreatestSumOfSubArray(int *pData, int nLength)
{
if ((pData == NULL) || (nLength <= 0))
{
g_InvalidInput = true;
return 0;
}

g_InvalidInput = false;

int nCurSum = 0;
int nGreatestSum = 0×80000000;
// 0×80000000是最小的int型(负)数，将nGreatestSum初始化为
// 最小的int值，是为了应对输入全负的情况

for (int i = 0; i < nLength; ++i)
{
if (nCurSum <= 0)
nCurSum = pData[i];
else
nCurSum += pData[i];

if(nCurSum > nGreatestSum)
nGreatestSum = nCurSum;
}

return nGreatestSum;
}

解法二：动态规划思想

用f(i)表示以第i个数字结尾的子数组的最大和，那么需要求出max[f(i)]。可用如下递归公式求f(i)：

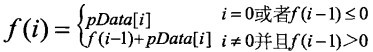
这个递归的求解可以优化为循环，具体与上面的代码一致。公式中的f(i)相当于变量nCurSum，而max[f(i)]就是nGreatestSum。

关于动态规划的入门可以参考：