二叉排序树(二叉搜索树)



二叉排序树(二叉搜索树)

二叉排序树

二叉排序树又称为二叉查找树，它是一种特殊结构的二叉树，其定义为：二叉树排序树或者是一棵空树，或者是具有如下性质的二叉树：

（1）若它的左子树非空，则左子树上所有结点的值均小于根结点的值；

（2）若它的右子树非空，则右子树上所有结点的值均大于根结点的值；

（3）它的左右子树也分别为二叉排序树。

这是一个递归定义。由定义可以得出二叉排序树的一个重要性质：中序遍历一个二叉排序树时可以得到一个递增有序序列。图1所示的二叉树就是一棵二叉排序树，若中序遍历图8.3（a）的二叉排序树，则可得到一个递增有序序列为：1，2，3，4，5，6，7，8，9。

 

    

 

 

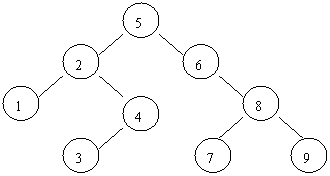
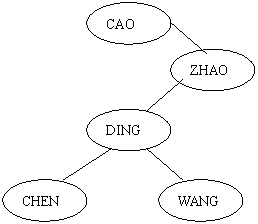
(a) 二叉排序树示例1                               (b) 二叉排序树示例2(根据字符ASCII码的大小)

图1二叉排序树

在下面讨论二叉排序树的操作中，使用二叉链表作为存储结构，其结点结构说明如下：

typedef struct node

{ KeyType key ; /*关键字的值*/

struct node *lchild,*rchild;/*左右指针*/

}bstnode,*BSTree;

 

1．二叉排序树的插入和生成

已知一个关键字值为key的结点s，若将其插入到二叉排序树中，只要保证插入后仍符合二叉排序树的定义即可。插入可以用下面的方法进行：1）若二叉树序树是空树，则key成为二叉树序树的根；2）若二叉树序树非空，则将key与二叉树序树的根进行比较，如果key的值等于根结点的值，则停止插入，如果key的值小于根结点的值，则将key插入左子树，如果key的值大于根结点的值，则将key插入右子树。

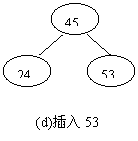
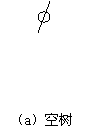
例如，设关键字的输入顺序为：45，24 ，53，12，28，90，按上述算法生成的二叉排序树的过程如图2所示。

 


 

 

 


 

 

 

 

 

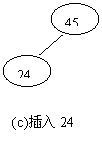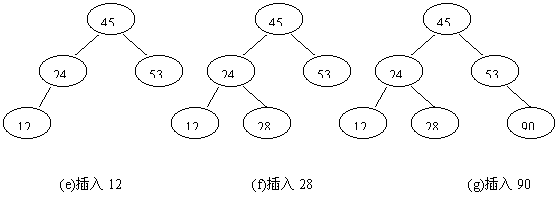
图2 二叉排序树的建立过程

对同样一些元素值，如果输入顺序不同，所创建的二叉树形态也不同。如上面的例子如果输入顺序为 24，53，90，12，28，45，则生成的二叉排序树如图3所示：

 

 

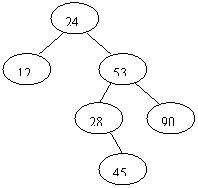
图3输入顺序不同所建立的不同二叉排序树

 2．二叉排序树的查找过程

由其定义可见，二叉排序树的查找过程为：
（1）若查找树为空，查找失败。
（2）查找树非空，将给定值key与查找树的根结点关键码比较。
（3）若相等，查找成功，结束查找过程，否则：
① 当给值key小于根结点关键码，查找将在以左孩子为根的子树上继续进行，转（1）。
② 当给值key大于根结点关键码，查找将在以右孩子为根的子树上继续进行，转（1）。


3．二叉排序树删除操作

从二叉排序树中删除一个结点之后，要求其仍能保持二叉排序树的特性。
设待删结点为*p（p为指向待删结点的指针），其双亲结点为*f，删除可以分三种情况，如图6-4所示。

 

（1）*p结点为叶结点，由于删去叶结点后不影响整棵树的特性，所以，只需将被删结点的双亲结点相应指针域改为空指针，如图6-4（a）所示。
（2）*p结点只有右子树或只有左子树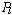，此时，只需将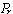或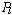替换*f结点的*p子树即可，如图6-4（b）、（c）所示。
（3）*p结点既有左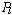子树又有右子树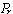，可按中序遍历保持有序地进行调整，如图6-4（d）、（e）所示。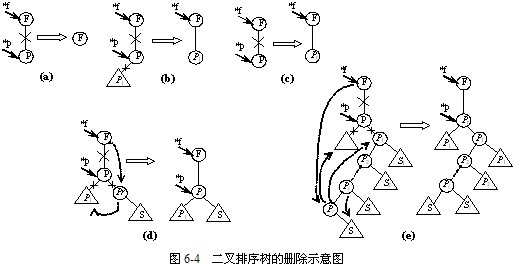

设删除*p结点前，中序遍历序列为：
① P为F的左子女时有：…，Pi子树，P，Pj，S子树，Pk，Sk子树，…，P2，S2子树，P1，S1子树，F，…。
② P为F的右子女时有：…，F，Pi子树，P，Pj，S子树，Pk，Sk子树，…，P2，S2子树，P1，S1子树，…。
则删除*p结点后，中序遍历序列应为：
① P为F的左子女时有：…，Pi子树，Pj，S子树，Pk，Sk子树，…，P2，S2子树，P1，S1子树，F，…。
② P为F的右子女时有：…，F，Pi子树，Pj，S子树，Pk，Sk子树，…，P2，S2子树，P1，S1子树，…。
有两种调整方法：
① 直接令Pi为*f相应的子树，以Pr为Pi中序遍历的最后一个结点Pk的右子树。
② 令*p结点的直接前驱Pr或直接后继（对Pi子树中序遍历的最后一个结点Pk）替换*p结点，再按（2）的方法删去Pr或Pk。
【算法分析】
对给定序列建立二叉排序树，若左右子树均匀分布，则其查找过程类似于有序表的折半查找。但若给定序列原本有序，则建立的二叉排序树就蜕化为单链表，其查找效率和顺序查找一样。因此，对均匀的二叉排序树进行插入或删除结点后，应进行调整，使其依然保持均匀。

程序代码实现：

  1. package binarytree;
  3. import java.util.ArrayDeque;
  4. import java.util.ArrayList;
  5. import java.util.List;
  6. import java.util.Queue;
  8. public class BinarySortTree<T extends Comparable<T>> {
  9.     //二叉搜索树，二叉排序树
  10.     public class Node{
  11.         T data;
  12.         Node parent;
  13.         Node lchild;
  14.         Node rchild;
  15.         public Node(T data,Node parent,Node lchild,Node rchild){
  16.             this.data=data;
  17.             this.parent=parent;
  18.             this.lchild=lchild;
  19.             this.rchild=rchild;
  20.         }
  21.         public boolean equals(Object obj){
  22.             if (this==obj) {
  23.                 return true;
  24.             }
  25.             if (obj.getClass()==Node.class) {
  26.                 Node target=(Node)obj;
  27.                 return data.equals(target.data)&&
  28.                         lchild==target.lchild&&
  29.                         rchild==target.rchild&&
  30.                         parent==target.parent;
  31.             }
  32.             return false;
  33.         }
  34.         @Override
  35.         public String toString() {
  36.             return ”Node [data="+data+"]“;
  37.         }
  39.     }
  41.     private Node root;
  43.     public BinarySortTree() {
  44.         root=null;
  45.     }
  46.     public BinarySortTree(T t) {
  47.         this.root = new Node(t, null, null, null);
  48.     }
  49.     //添加节点
  50.     public void add(T element){
  51.         if (root==null) {
  52.             root=new Node(element, null, null, null);
  53.         } else {
  54.             Node current=root;
  55.             Node parent=null;
  56.             int cmp=0;
  57.             //搜索合适的叶子节点，以该叶子节点为父节点添加新节点
  58.             do {
  59.                 parent=current;
  60.                 cmp=element.compareTo(current.data);
  61.                 if (cmp>0) {
  62.                     current=current.rchild;
  63.                 } else {
  64.                     current=current.lchild;
  65.                 }
  66.             } while (current!=null);
  67.             //创建新节点
  68.             Node newNode=new Node(element, parent, null, null);
  69.             if (cmp>0) {
  70.                 parent.rchild=newNode;
  71.             } else {
  72.                 parent.lchild=newNode;
  73.             }
  74.         }
  75.     }
  76.     //删除节点
  77.     public void remove(T element){
  78.         //获取要删除的节点
  79.         Node target=getNode(element);
  80.         if (target==null) {
  81.             return;
  82.         }
  83.         //左、右子树是否为空
  84.         if (target.lchild==null&&target.rchild==null) {
  85.             if (target==root) {
  86.                 root=null;
  87.             } else {
  88.                 if (target==target.parent.lchild) {
  89.                     target.parent.lchild=null;
  90.                 } else {
  91.                     target.parent.rchild=null;
  92.                 }
  93.                 target.parent=null;
  94.             }
  95.         } else if(target.lchild==null&&target.rchild!=null){
  96.             if (target==root) {
  97.                 root=target.rchild;
  98.             } else {
  99.                 if (target==target.parent.lchild) {
  100.                     target.parent.lchild=target.rchild;
  101.                 } else {
  102.                     target.parent.rchild=target.rchild;
  103.                 }
  104.                 target.rchild.parent=target.parent;
  105.             }
  106.         }else if(target.lchild!=null&&target.rchild==null){
  107.             if (target==root) {
  108.                 root=target.lchild;
  109.             } else {
  110.                 if (target==target.parent.lchild) {
  111.                     target.parent.lchild=target.lchild;
  112.                 } else {
  113.                     target.parent.rchild=target.lchild;
  114.                 }
  115.                 target.lchild.parent=target.parent;
  116.             }
  117.         }else {
  118.             Node lchildMaxNode=target.lchild;//存放左孩子最大的节点
  119.             while (lchildMaxNode.rchild!=null) {
  120.                 lchildMaxNode=lchildMaxNode.rchild;
  121.             }
  122.             lchildMaxNode.parent.rchild=null;
  123.             lchildMaxNode.parent=target.parent;
  125.             if (target==target.parent.lchild) {
  126.                 target.parent.lchild=lchildMaxNode;
  127.             } else {
  128.                 target.parent.rchild=lchildMaxNode;
  129.             }
  130.             lchildMaxNode.lchild=target.lchild;
  131.             lchildMaxNode.rchild=target.rchild;
  132.             target.parent=target.lchild=target.rchild=null;
  133.         }
  134.     }
  135.     //获取要指定的节点
  136.     public Node getNode(T element) {
  137.         Node p=root;
  138.         while (p!=null) {
  139.             int cmp=element.compareTo(p.data);
  140.             if (cmp>0) {
  141.                 p=p.rchild;
  142.             } else if (cmp<0) {
  143.                 p=p.lchild;
  144.             }else {
  145.                 return p;
  146.             }
  147.         }
  148.         return null;
  149.     }
  150.     //广度优先遍历
  151.     public List<Node> breadthFrist(){
  152.         Queue<Node> queue=new ArrayDeque<Node>();
  153.         List<Node> list=new ArrayList<Node>();
  154.         if (root!=null) {
  155.             queue.offer(root);
  156.         }
  157.         while (!queue.isEmpty()) {
  158.             list.add(queue.peek());
  159.             Node pNode=queue.poll();
  160.             if (pNode.lchild!=null) {
  161.                 queue.offer(pNode.lchild);
  162.             }
  163.             if (pNode.rchild!=null) {
  164.                 queue.offer(pNode.rchild);
  165.             }
  166.         }
  167.         return list;
  168.     }
  169. }